Coursera 吴恩达机器学习入门课笔记（更新至第三课）

吴恩达在 Coursera 上的机器学习入门课的笔记。只给自己看，所以写得非常简略。

使用的是较新的 2022 版本（和之前的不太一样），双语可见 BV1Pa411X76s。

第一课

线性回归（Linear Regression）

设特征数为 $n$，样本数为 $m$。

模型：$f_{\text{w}, b}(\text{x}) = \text{w}\text{x} + b = \left(\sum_{i = 1}^n w_ix_i\right) + b$

损失函数：

$$L(f_{\text{w}, b}(\text{x}^{(i)}), y^{(i)}) = (f_{\text{w}, b}(\text{x}^{(i)}) - y^{(i)})^2$$

费用函数：

$$J(\text{w}, b) = \frac 1{2m} \left(\sum_{i = 1}^m \left(f_{\text{w}, b}(\text{x}^{(i)}) - y^{(i)} \right)^2 \right) + \frac \lambda{2m} \sum_{i = 1}^n w_i^2$$

此处 $\frac \lambda{2m} \sum_{i = 1}^n w_i^2$ 采用了正则化（Regularization），能使得 $w_i$ 的值减小，从而抑制过拟合（Overfitting）。

梯度下降（Gradient Descent）

$$
\begin{aligned}
\frac {\partial J(\text{w}, b)}{\partial w_j} &= \frac 1m \left(\sum_{i = 1}^m \left( f_{\text{w}, b}(\text{x}^{(i)}) - y^{(i)} \right) x_j^{(i)} \right) + \frac 1m w_j \
\end{aligned}
$$

$$
\begin{aligned}
\frac {\partial J(\text{w}, b)}{\partial b} &= \frac 1m\sum_{i = 1}^m \left( f_{\text{w}, b}(\text{x}^{(i)}) - y^{(i)} \right) \
\end{aligned}
$$

特征缩放（Feature Scaling）

• Mean Normalization：$x’ = \frac {x - \mu}{\max - \min}$
• Z-Score Normalization：$x’ = \frac {x - \mu}\sigma$

目标是让 $x$ 尽可能趋近于 $[-1, 1]$ 分布。

逻辑回归（Logistic Regression）

Sigmoid：$f(x) = \frac 1{1 + e^{-x}}$

ReLU：$f(x) = \max{0, x}$

模型：$f_{\text{w}, b}(\text{x}) = \text{sigmoid}\left(\left(\sum_{i = 1}^n w_ix_i\right) + b\right)$

也可以换成 ReLU。

损失函数：

$$
L(f_{\text{w}, b}(\text{x}^{(i)}), y^{(i)}) =
\begin{cases}
-\log\left(f_{\text{w}, b}(\text{x}^{(i)})\right), y^{(i)} = 1\
-\log\left(1 - f_{\text{w}, b}(\text{x}^{(i)})\right), y^{(i)} = 0 \
\end{cases}
$$

实际操作中，使用该损失函数比直接套用线性回归的损失函数更优。

第二课

输出层的转换函数选择

• 二元分类：$\text{Sigmoid}$
• 回归：$\text{id}$（带正负）或 $\text{ReLU}$（非负）

Softmax 回归

Softmax 回归用来解决多分类问题。

假设类别共有 $k$ 种，则 Softmax 回归的输出为一个 $k$ 维向量 $\text{x}$，$x_i$ 衡量分类为 $i$ 的相对可能性有多大。实际分类为 $i$ 的概率估计为

$$a_i = P(y = i) = \frac {e^{x_i}}{\sum_{j = 1}^k e^{x_j}}$$

损失函数为

$$
loss({a_k}, y) = -\log a_y
$$

交叉验证

咕了

决策树解决二分类问题

给定特征向量 $\text{x} = {a_1, a_2, \ldots, a_k} \ (a_i \in {0, 1})$，估计其分类 $\hat y \in {0, 1}$。

熵：若 $p$ 为当前节点数据中第一类的占比，那么定义熵 $H(p)$ 为

$$H(p) = -p \log_2 p - (1 - p) \log_2 (1 - p), \quad p \in (0, 1)$$

特别地，$H(0) = H(1) = 0$（这是因为 $\log_2 0$ 没有定义）。可以注意到 $\lim_{x \rightarrow 0} x \log_2 x = 0$，因此即使特殊定义 $H(0) = 0\log_2 0 = 0$ 也不会破坏函数连续性。

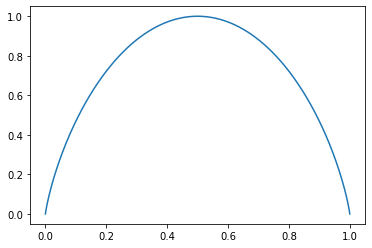
信息增益：若将根节点 $root$ 分为左子树 $left$ 和右子树 $right$，记节点数据个数为 $n$，则信息增益（Information Gain，实际上就是熵减）为

$$H(p^{root}) - \frac {n^{left}}{n^{root}} H(p^{left}) - \frac {n^{right}}{n^{root}} H(p^{right})$$

取信息增益最大分割即可。

停止条件

停止划分的条件有几种：

• 当当前节点深度已经达到规定的最大深度时；
• 当最大信息增益小于某个阈值时；
• 当节点数据数小于某个阈值时。

One-hot 编码

对于 $a \in [1, n] \cup \N$，可以将 $a$ 转化为一个长度为 $n$ 的向量 $\vec b = {[a = 1], [a = 2], [a = 3], \ldots, [a = n]}$。可以注意到，转化后的 $\vec b$ 的每个元素都为 $0$ 或 $1$，并且有且仅有一个元素为 $1$（因此成为 One-hot 编码）。

对多分类问题的决策树应用 One-hot 编码，即可转化为二分类问题。

连续取值

在决策树上，对于取值为实数的特征进行分割时，可以取条件为 $x \leq C$。

若当前有 $m$ 个数据，其从小到大为 $x_1 \leq x_2 \leq \ldots \leq x_m$，则可以考虑取 $C = \frac {x_i + x_{i + 1}}2 \quad (1 \leq i \leq n - 1)$。

扩展到回归树

回归树和决策树类似，但其输出为一个 $y \in \R$，而不是预测其分类。

类似地，可以定义回归树的信息增益为

$$D(p^{root}) - \frac {n^{left}}{n^{root}} D(p^{left}) - \frac {n^{right}}{n^{root}} D(p^{right})$$

其中 $D$ 为方差函数。

决策树森林

单棵决策树对数据的微小改变较为敏感。为了使其更加健壮，可以生成多棵决策树，然后收集所有决策树计算后的结果，取众数作为结果返回。

生成决策树的方式是：每次有放回抽样，抽出与数据集大小个数相等的样本（这些样本可重复），根据它们建决策树。

决策树棵数一般在 $100$ 左右，因为每增加一棵决策树，其对准确率的增加是有边际递减的。一般来讲，当超过 $100$ 之后其对性能的提升就很小了，还会减慢计算速度。

随机森林算法

仅有放回抽样构造出的决策树，在根节点附近的分类标准仍然是高度相似的。记特征数为 $n$，为了更加随机，可以在每次分割时仅随机选出 $k < n$ 个特征进行判断，取信息增益最多的那个进行分割。

一般来讲取 $k \approx \sqrt n$（西瓜书上据说 $k \approx \log_2 n$）。

Boost

更进一步地，在每次抽样时，我们可以更有意识（更高概率地）抽出那些被当前已有决策树森林错误分类的样本。

XGBoost

XGBoost 是一个开源高效的决策树 / 回归树计算库。

决策树 Vs. 神经网络

决策树的优点：

• 适合处理天然结构化的数据。简单来说，如果数据看起来像一个表格，则适合用决策树处理。
• 训练时间短。
• 较小的决策树可能是 Human-interpretable（人类可以理解的）。

决策树的缺点：

• 不适合处理非结构化数据（图像，文本，视频，音乐等）。

神经网络的优点：

• 适合处理几乎所有类型的数据（无论是否结构化）。
• 可以和迁移学习（Tranfer learning）一起使用。
• (*) 可以更容易做到让多个机器学习模型一起配合训练。
  • 原因很复杂，暂时不展开。

神经网络的缺点：

• 训练时间长。

第三课

引入

• 无监督学习算法
  • 聚类（Clustering）
  • 异常检测（Anormaly detection）
• 推荐系统
• 强化训练

K-means 聚类算法

K-means 算法可以用来解决聚类问题。算法流程如下：

1. 随机 $k$ 个点的坐标 $\text{p}_1, \text{p}_2, \ldots, \text{p}_k$作为 $k$ 个簇的中心点。
2. 重复以下流程直至中心点坐标无变化：
   1. 遍历所有数据点，将每个数据点分配给离它最近的那个中心点。
   2. 将中心点坐标改为它所支配的数据点坐标的平均值。

其中若中心点无支配数据点，则要么删去该中心点，要么重新随机中心点坐标。

上面的做法实际上是在优化代价函数

$$J({c^{(m)}}, {\text{p}k}) = \frac 1m \sum{i = 1}^m | \text{x}^{(i)} - \text{p}_{c^{(i)}}|^2$$

该代价函数也称为 Distortion 函数。

可以注意到，算法流程中的 2.1. 既是在保持 ${\text{p}_k}$ 不变的前提下解得 ${c^{(m)}}$ 的最优解，2.2 既是在保持 ${c^{(m)}}$ 不变的前提下解得 ${\text{p}_k}$ 的最优解。也就是说，每一步调整后，代价函数的值都应减小或不变。

K-means 聚类算法的改进

初始化时，我们可以令 $k$ 个中心点坐标为 $k$ 个不同的样本数据，以取得更好的效果。

另外，该代价函数也有多个局部最小值，所以我们也可以运行多次 K-means 算法（一般为 $50 \ldots 1000$ 次），取代价函数最小的作为答案。

如何选择 K 值

肘部法则（Elbow Method）：令 $f(k)$ 为取 $K = k$ 时计算得到的最小代价，则取 $f(k) - k$ 图像上明显的拐点的横坐标作为 $k$ 的取值。但实际上不少时候这个图像是比较平缓的，所以其实也没有很大用处，吴恩达也说自己不用。

实际应用中，该算法一般是用来产生一些簇，提供给下游（Downstream）的开发人员，让他们进一步进行计算的。所以可以考虑根据下游开发人员的反馈调整 $K$ 值。

注意：你并不是在选择 $k$ 使得 $f(k)$ 最小。实际上，大多数情况下 $f(k)$ 随着 $k$ 的增大是近似单调下降的，但这并不意味着簇数越多越好。

异常检测

给出 $m$ 个向量 ${\text{x}^{(i)}}$ 作为参考，再给出一个向量 $\text {x}$，判断其对这 $m$ 个向量来说正不正常。

先强行假定每一维的参数是相互独立的，然后我们考虑用正态分布估计每一维参数的分布。计算

$$\mu_j = \frac 1n \sum_{i = 1}^m x_j^{(i)}$$

$$\sigma_j^2 = \frac 1n \sum_{i = 1}^m (x_j^{(i)} - \mu_j)^2$$

则可以估计给定的参数 $x_j$ 正常的概率是 $p(x_j; \mu_j, \sigma_j^2)$，此处的 $p(\ldots)$ 为正态分布概率函数。

由于互相独立，可以得知

$$p(\text{x}) = \prod_{j = 1}^k p(x_j; \mu_j, \sigma_j^2)$$

若 $p(\text{x}) < \epsilon$（其中 $\epsilon$ 为我们指定的一个常数），则认为 $\text{x}$ 是异常的。

异常检测的交叉验证

• 训练集 ${\text{x}^{(m)}}$：用于训练
• 交叉验证集 ${(\text{x}{cv}^{(m{cv})}, y_{cv}^{(m_{cv})})}$：用于选择模型
• 测试集 ${(\text{x}{test}^{(m{test})}, y_{test}^{(m_{test})})}$：用于检验模型的实际正确率

注意要点：

• 一般异常数据数远小于正常数据数（如 $1:200$）。
• 一般不需要把异常数据放入训练集，而应当放入交叉验证集和测试集。
• 若异常数据极其少（只有一两个），可考虑不适用测试集（但会带来一定的风险）。

异常检测 Vs. 监督学习

异常检测适用于：

• 异常数据极其少的时候（例如不超过 $20$）。
• 有很多种异常类型，即很难从异常数据习得其通性的时候。
  • 异常检测算法会将与正常数据偏离较大的数据当作异常，监督学习会将与异常数据相近的当作异常。也就是说，如果出现了一种新的异常类型，异常检测算法会将其视为异常（因为与正常偏离大），而监督学习不会将其视为异常（因为与异常距离远）。

监督学习则相反。

例如，金融欺诈的手段千变万化，因此更适合用异常检测；垃圾邮件的类别则相对少，因此更适合用监督学习。

特征选择

监督学习中，即使选择了一些无关特征，算法仍然可以自动调整它们的权值，使它们对结果不起作用。

但异常检测中，特征的选择极其重要。

首先，可以将特征处理一下，使得它们更加符合正态分布，例如

• $f(x) = \ln (x + C)$
• $f(x) = x^a$

尽管有些方法可以自动测量其与正态分布的相近程度，但在实践中作用不大。实践中，多尝试几个 $C$ 和 $a$ 即可。

其次，可以对实际数据作误差分析。例如，如果算法运行不优，大概率是异常数据和正常数据的 $p(\text{x})$ 大小相近。此时可以查看异常数据，分析是否有什么先前没有考虑到的特征是与大部分正常数据相离的。你也可以试着组合一些特征来产生新特征。

推荐系统：协同过滤（Collaborative filtering）

有 $n_u$ 个用户，$n_m$ 个商品，记 $r(i, j) \in {0, 1}$ 表示用户 $j$ 是否给商品 $i$ 评分，令 $y^{(i, j)}$ 表示其评分。

已知部分评分情况，预估用户对每个未评分商品的评分是多少。

可设商品 $i$ 有隐藏的 $n$ 维特征向量 $\text{x}^{(i)}$，用户 $j$ 的线性回归参数为 $\text{w}^{(j)}, b^{(j)}$，则预计评分为

$$\hat y^{(i, j)} = \text{w}^{(j)}\text{x}^{(i)} + b^{(j)}$$

类似地，定义代价函数

$$J({\text{x}^{(n_m)}}, {\text{w}^{(n_u)}}, {b^{(n_u)}}) = \frac 12\sum_{r(i, j) = 1} \left(\text{w}^{(j)}\text{x}^{(i)} + b^{(j)} - y^{(i, j)}\right)^2 + \frac \lambda 2 \sum_{j = 1}^{n_u} \left(\text{w}^{(j)}\right)^2 + \frac \lambda 2 \sum_{i = 1}^{n_m} \left(\text{x}^{(i)}\right)^2$$

用梯度下降最优化 $J(\ldots)$ 即可。

对于二分类预测问题（即 $y^{(i, j)} \in {0, 1}$），可以用逻辑回归的方法类似处理，此处不再赘述。

均值归一化

设 $\mu_i$ 为商品 $i$ 的平均评分，可以令所有 $y^{(i, j)}$ 减去 $\mu_i$ 后进行拟合。训练到最后输出时再在预测值上加上 $\mu_i$ 即可。

这样的好处是当用户评分过极少的电影时，算法表现也会更好。

寻找共同点

可以通过协同过滤算法求解出的 ${\text{x}^{(i)}}$，用 $|\text{x}^{(j)} - \text{x}^{(i)}|^2$ 来判断商品 $i, j$ 的相似度。

协同过滤的局限

• 存在冷启动问题：对于新注册的用户 / 新上架的商品，算法无法提供良好的推荐。
• 难以利用已知特性：即使拥有一些已知特性，它们也较难显著提高协同过滤算法的表现。

基于内容过滤（Content-based filtering）

协同过滤算法会根据那些给出评分和你相似的用户，来提供相近的推荐。而基于内容过滤算法，则会根据用户和商品的特征来提供推荐。

设用户 $j$ 的偏好特征为 $\text{x}_u^{(j)}$，商品 $i$ 的特征为 $\text{x}_m^{(i)}$（**$\text{x}_u^{(j)}, \text{x}_m^{(i)}$ 维度不一定相等），基于内容过滤算法会根据 $\text{x}_u^{(j)}$ 计算一个转化后的特征向量 $\text{v}_u^{(j)}$，根据 $\text{x}_m^{(i)}$ 计算 $\text{v}_m^{(i)}$（$\text{v}_u^{(j)}, \text{v}_m^{(i)}$ 维度必须相等**），并预估评分为

$$\hat y^{(i, j)} = \text{v}_u^{(j)}\text{v}_m^{(i)}$$

此处和之前的算法相比少了常数项，但实际证明，缺少常数项几乎不会影响算法性能。

实现基于内容过滤算法的一个方式是深度学习。构建两个神经网络 $f: \R^{k_u} \rightarrow \R^{k_v}$ 和 $g: \R^{k_m} \rightarrow \R^{k_v}$，令 $\text{v}_u^{(j)} = f(\text{x}_u^{(j)}), \text{v}_m^{(i)} = g(\text{x}_m^{(i)})$，我们需要训练 $f, g$ 使得其产生的预估良好。

实际上，我们可以把两个神经网络结合起来。把 $\text{x}_u^{(j)}, \text{x}_m^{(i)}$ 首尾相连成为一个输入，并在 $f, g$ 的最后用一个神经元连接起来，输出其点积作为结果。这样一来，我们只需要训练一个神经网络，问题会变得简单许多。

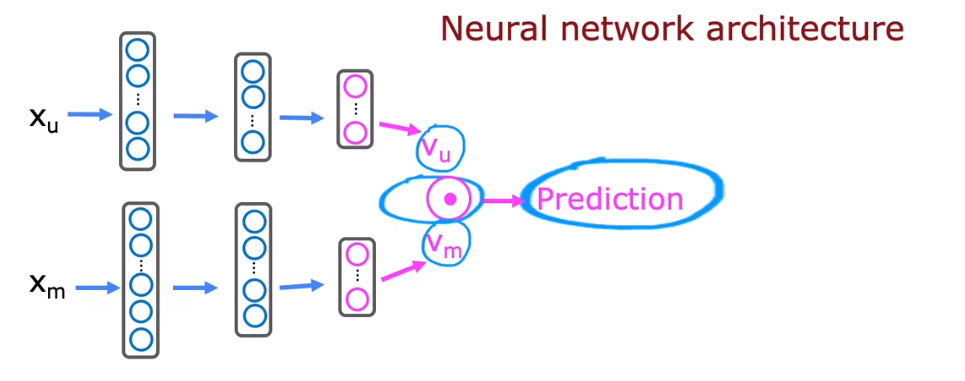
先前提到说，神经网络相比决策树的好处是容易将多个神经网络结合起来使用。这就是一个鲜明的例子。

费用函数和先前的类似，也是差值平方和加上正则化项。

从大目录里推荐

现代网站通常拥有大量的资源，例如超过十万甚至百万首曲库。对于每个用户都强行枚举所有商品并放入神经网络计算是不现实的。

许多大规模推荐系统的实现可以分为两个步骤：数据检索和排名。即，检索出十几或几百个该用户可能感兴趣的商品，然后放入神经网络计算并排序。

推荐系统的危害

推荐系统并不完全是好东西，滥用它可能会造成一些不理想的效果：

• 信息茧房。
• 激化仇恨 / 引战言论，因为它们能更好地吸引读者注意。
• 公司的算法推荐的商品可能不是对用户最好的，而是对公司利益最大化的

尽力去做有益于人民的东西。

强化学习引入

强化学习的一些应用：

• 训练机器人
• 工厂优化（任务调度安排）
• 金融股票交易
• 游戏

原理：程序可以任意进行行动，算法仅指定某些状态的奖励，让程序自己学习如何最大化奖励（训狗）。

形式化描述：程序任意时刻都可以用四个参数 $(s, a, R(s), s’)$ 描述，其中：

• $s$ 为当前状态
• $a$ 为行动
• $R(s)$ 为当前奖励
• $s’$ 为后继状态

回报和策略

为了让程序更快地拿到更多奖励，每秒程序的奖励会衰减，即乘上一个略小于 $1$ 的正实数 $\gamma$（称为折扣系数）。

程序至当前为止所获得的所有奖励，乘上对应折扣系数的次幂之和称为回报（Return）。

我们希望求出一个策略（Policy）函数 $\pi: s \rightarrow a$，表示当状态为 $s$ 时应当采取行动 $a$。